สวัสดีท่านผู้เข้าชมเว็บไซต์ของ บริษัท อีบิลด ครับ เมื่อวันศุกร์ที่ 3 มิ.ย ที่ผ่านมาทางทีมงานของบริษัทได้มีโอกาสไปร่วมงาน การสัมมนาของบริษัท แปซิฟิกไพพ์ จำกัด (มหาชน) เกี่ยวกับเรื่อง การออกแบบจุดต่อโครงสร้างเหล็กประเภทท่อไม่ยากอย่างที่คิด”จากท่าน ผศ.ดร. พิสณฑ์ อุดมวรรัตน์  (ภาควิชาวิศวกรรมโยธา มหาวิทยาลัยเทคโนโลยีพระจอมเกล้าพระนครเหนือ) พอฟังหัวข้อแล้วท่านผู้เข้าชมเว็บไซต์ คงคิดว่าการที่จะออกแบบจุดต่อของโครงสร้างเหล็กนั้นอาจทำโดยไม่ต้องคำนวณหรือต้องทำอะไรให้มันยุ่งยากใช่ใหมครับซึ่งเป็นความคิดที่ผิดมากๆครับการที่จะออกแบบก่อสร้างที่เกี่ยวกับจุดต่อโครงสร้างเหล็กที่ถูกต้องนั้นไม่ใช่แค่ออกแบบเพื่อความสวยงามอย่างเดียวแต่ต้องผ่านการคำนวณและออกแบบเพื่อความมั่งคงของงานก่อสร้างนั้นๆด้วยครับเช่นข้อมูลดังต่อไปนี้ครับ

Hollow Sections

-ท่อเหล็กหน้าตัดกลม Circular Hollow Sections (CHS)

-ท่อเหล็กหน้าตัดสีเหลี่ยมผืนผ้า Rectangular Hollow Sections (RHS)

-ท่อเหล็กหน้าตัดสี่เหลี่ยมจัตุรัส Square Hollow Sections (SHS)

การผลิตท่อเหล็ก Hollow Sections

1.ท่อที่ผลิตโดยการเชื่อมเหล็กแผ่นโดยอาศัยความต้านทานไฟฟ้า (Electric Resistance Welding, ERW)

2.ท่อเชื่อมแนวตะเข็บตรงแบบ Arc Welding เช่น Double Submerged Arc Weld (DSAW) Pipe

3.ท่อเชื่อมแบบ Spiral

4.ท่อไร้ตะเข็บ (Seamless pipe)

คุณสมบัติของเหล็กโครงสร้างประเภทท่อ สามารถอ้างอิงตามมาตรฐานในประเทศและต่างประเทศดังนี้

ASTM ,BS ,JIS ,TIS ,Europe (Eurocode) มาตาฐาน CIDECT และ Eurocode 3 ได้ให้คำแนะนำในการออกแบบเบื้องต้นไว้ดังนี้

1.สำหรับการออกแบบโครงสร้างแบบโครงถัก (Lattice structure) ผู้ออกแบบสามารถ สมมุติให้จุดต่อเป็นแบบจุดหมุน (Pin joint)โดยไม่ต้องคำนึงถึงค่าโมเมนต์ดัด อันดับสอง(Secondary bending moment) ที่เกิดขึ้นจาก Stiffnessของจุดต่อถึงแม้ว่าจุดต่อนั้นๆ มีความสามารถในการต้านทานการหมุนเพียงพอตามทฤษฎีทางสถิตยศาสตร์ แต่ในทางปฏิบัติในงานโครงสร้างโครงถักจริงนั้น อาจเกิดการเยื้องศูนย์ขององค์อาคาร ที่จะทำให้จุดต่อของโครงสร้างไม่เป็นไปตามสมมุติฐานของจุดต่อที่เป็นแบบจุดหมุน

ดังนั้น Erocode3 จึงกำหนดขอบเขตของจุดตัดของท่อแกนรองซึ่งสามารถเยื้องศูนย์โดยวัดจากแนวแกนของท่อแกนหลักถ้าจุดต่อมีการเยื้องศูนย์อยู่ภายใต้ข้อกำหนด -0.55≤e/d0≤0.25 หรือ-0.55≤e/h0≤0.25 และเกิดแรงดึงภายในท่อแกนหลักโมเมนต์ที่เกิดขึ้นในจุดต่อไม่จำเป็นต้องนำมาพิจารณา ในกรณีที่เกิดแรงอัดภายในท่อแกนหลักอาจทำให้เกิดโมเมนต์กระทำบนท่อแกนหลักซึ่งมีผลต่อกำลังของจุดต่อ ฉะนั้นจำเป็นต้องทำการตรวจสอบระยะเยื้องศูนย์เพื่อคำนวณหาโมเมนต์ที่เกิดขึ้น

2.จุดต่อแบบมีช่องว่างระหว่างท่อแกนรอง (Gap joint) จะเป็นจุดต่อที่ได้รับความนิยมมากกว่าจุดต่อที่ไม่มีช่องว่างหรือจุดต่อแบบซ้อนทับกันของท่อแกนรอง (Overlap joint) เนื่องจากการเตรียมชิ้นงานและการประกอบทำได้ง่ายกว่าโดยเฉพาะการตัดปลายท่อในทางกลับกันคุณสมบัติเด่นของจุดต่อแบบซ้อนทับคือ มีความแข็งแรงของจุดต่อมากกว่าจุดต่อแบบมีช่องว่างโดยเฉพาะอย่างยิ่งจุดต่อแบบซ้อนทับเต็มหน้า (Fully overlap joint) โดยปกติแล้วระยะช่องว่างระหว่างท่อแกนรอง (g) จะวัดจากระยะบนผิวท่อแกนหลักระหว่างท่อแกนรองไม่รวมระยะขาลอยเชื่อม ในการออกแบบจุดต่อแบบมีช่องว่างที่ดีจะต้องมีช่องว่าง g≥t1+t2 จะทำให้รอยเชื่อมไม่ซ้อนทับกัน สำหรับจุดต่อแบบซ้อนทับ จะต้องมีเปอร์เซ็นต์ของการซ้อนทับของแกนรอง Ov≥25% เพื่อที่มันใจได้ว่าระยะซ้อนทับของท่อแกนรองมีขนาดกว้างเพียงพอและสามารถส่งถ่ายแรงเฉือนจากท่อแกนรองด้านหนึ่งไปยังอีกด้านหนึ่งได้

3.โครงสร้างแบบ Lattice structures เช่น โครงถัก ปริมาณวัสดุที่ใช้โดนน้ำหนักประมาณ 50% ของทั้งหมดจะเป็นของท่อแกนหลักรับแรงอัด ประมาณ 30% จะเป็นของท่อแกนหลักรับแรงดึงและอีกประมาณ 20% จะเป็นของท่อแกนรองยึดระหว่างท่อแกนหลัก นั้นเพื่อการประหยัด ท่อแกนหลักรับแรงอัดควรจะเป็นชนิดผนังบาง (Thin wall section) ท่าที่จะเป็นไปได้ และเพื่อป้องกันการเกิดสนิมในโครงถักควรเลือก หน้าตัดที่มีผิวด้านนอกให้น้อยที่สุดเพื่อลดการทาป้องกันสนิม

4.การเพิ่มความแข็งแรงของจุดต่อโดยการลดขนาดหน้าตัดท่อแกนหลักหรือลดอัตราส่วน d/t และเพิ่มอัตราส่วน ความหนา t0/t1 สำหรับท่อแกนหลักที่รับแรงอัดควรจะพิจารณาความสมดุลระหว่างความแข็งแรงของจุดต่อและความต้านทานของการเกิดการโก่งเดาะ โดยให้มีความแข็งแรงที่สุดเท่าที่จะทำได้ในส่วนของท่อแกนหลักรับแรงดึง ควรพิจารณาเลือกอัตราส่วน d/t หรือ b/t ให้มีค่าน้อยที่สุดเท่าที่จะเป็นไปได้

5.ในการพิจารณาประสิทธิภาพความแข็งแกร่งของจุดต่อ (ความแข็งแรงของจุดต่อหารด้วยแรงกระทำ ณ จุดครากของท่อแกนรอง Ai*Fyi) จะเพิ่มขึ้นตามอัตราส่วนความหน้าท่อแกนหลักต่อท่อแกนรอง t0/t1 ซึ่งควรเลือกให้มีค่ามากสุดเท่าที่จะเป็นไปได้โดยปกติควรมีค่ามากกว่า 2 เท่า

6.ความแข็งแรงของจุดต่อยังขึ้นอยู่กับอัตราส่วนของหน่วยแรงที่จุดครากของท่อแกนหลักต่อท่อแกนรอง การใช้เหล็กที่มีกำลังสูงขึ้นสำหรับท่อแกนหลักอาจจะสามารถประหยัดต้นทุนได้มากขึ้น ทั้งนี้จะต้องพิจารณาถึงความเป็นไปได้ในทางปฏิบัติด้วย

แบบจำลองเพื่อการวิเคราะห์พฤติกรรมจุดต่อ

แบบจำลองเพื่อการวิเคราะห์พฤติกรรมจุดต่อมีวัตถุประสงค์เพื่อใช้อธิบายพฤติกรรมของจุดต่อใต้แรงกระทำและเพื่อใช้ทำนายกำลังรับแรงสูงสุดของจุดต่อรูปแบบการวิบัติของจุดต่อประเภทท่อกลมอาจพิจารณาเพียงบางรูปได้แก่ การเกิดพลาสติกที่ผนังท่อแกนหลัก (Chord plastification) การเฉือนทะลุของผนังท่อแกนหลัก (Chord punching shear failure) และการเฉือนครากของท่อแกนหลัก (Chord shear failure) แบบจำลองเพื่อการวิเคราะห์พฤติกรรมของจุดต่อที่เกี่ยวข้องมีดังนี้

-แบบจำลองวงแหวน (Ring model for Chord plastification)

-แบบจำลองการเฉือนทะลุของท่อแกนหลัก (Punching shear model for chord punching shear)

-แบบจำลองการเฉือนครากของท่อแกนหลัก (Chord shear model)

สมการการออกแบบและข้อกำหนดของการออกแบบจุดต่อโครงสร้างเหล็กประเภทท่อกลม
 

การพัฒนาสูตรหรือสมการสำหรับการออกแบบยังคงใช้แบบจำลองวงแหวน (Ring model) เป็นสมการพื้นฐาน ซึ่งรูปแบบทั่วไปของสมการจุดต่อ แบบ T Y X K และ N

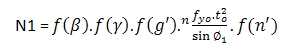
กำลังของจุดต่อจะขึ้นอยู่กับการวิบัติแบบพลาสติกของท่อแกนหลักเป็นสำคัญแต่จำเป็นต้องตรวจสอบการวิบัติแบบเฉือนทะลุเพิ่มเติม สำหรับการตรวจสอบวิบัติแบบเฉือนครากของแกนหลักอาจไม่จำเป็นเมื่อพารามิเตอร์ของจุดต่อยังคงอยู่ภายในขอบเขตที่กำหนด

สมการการออกแบบจุดต่อโครงสร้างเหล็กประเภทท่อสี่เหลี่ยมผืนผ้า

ชนิดจุดต่อ T Y และ X




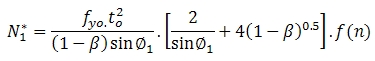
เมื่อ β = 1.0




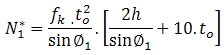
เมื่อ 0.85<β≤1.0 จะต้องเทียบค่าเชิงเส้นระหว่างที่คำนวณได้จาก Chord face yielding และ Chord side wall failure

เมื่อ β>0.85 Effective width

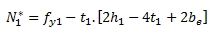
เมื่อ 0.85≤β≤1-1/y  Punching shear

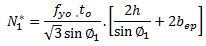
สมการการออกแบบจุดต่อโครงสร้างเหล็กประเภทท่อสี่เหลี่ยมจัตุรัส

ชนิดจุดต่อ T Y และ X

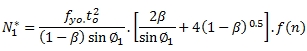
ชนิดจุดต่อแบบ K และ N ชนิดมีช่องว่าง β≤1.0  Chord face plastification

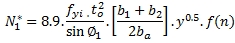
ตัวอย่างการออกแบบจุดต่อโครงสร้างเหล็กประเภทท่อสี่เหลี่ยมผืนผ้า

ตัวอย่าง จงตรวจสอบจุดต่อโครงสร้างเหล็กประเภทท่อสี่เหลี่ยมผืนผ้าแบบ K ชนิดมีช่องว่างระหว่างท่อแกนรองดังนี้

ท่อแกนหลัก ; RHS 200x150x9.0 mm

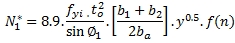
ท่อแกนรอง 1; RHS 150x100x9.0 mm

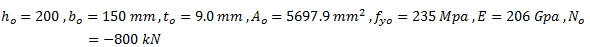
ท่อแกนรอง 2; RHS 150x100x9.0 mm

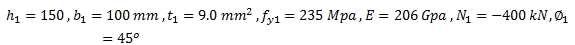
Gap=18 mm.

คำนวณหาค่าพารามิเตอร์

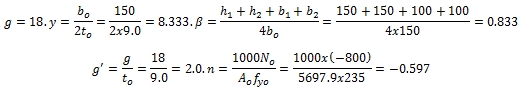
ตรวจสอบค่าพารามิเตอร์

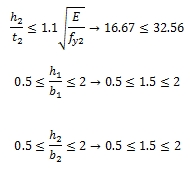
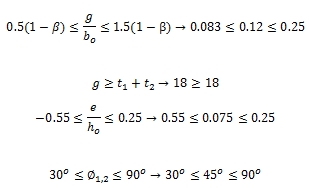
คำนวณค่าฟังก์ชั่น

1.การตรวจสอบ Chord face plastification

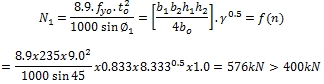
2.การตรวจสอบ Chord shear

3.การตรวจสอบ Effective width

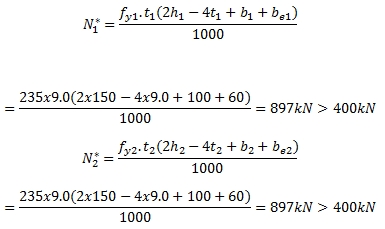
4.การตรวจสอบ Punching shear

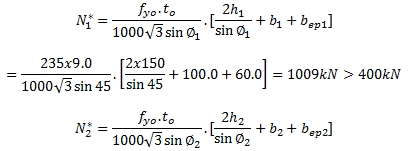
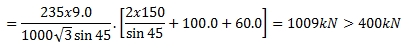
ตัวอย่างการออกแบบจุดต่อโครงสร้างเหล็กประเภทท่อกลม

จงออกแบบจัดต่อโครงสร้างเหล็กประเภทท่อกลมแบบ K ชนิดมีช่องว่างระหว่างท่อแกนรองดังนี้ ท่อแกนหลัก; CHS 300x10.3 mm. ท่อแกนรอง 1; CHS 300x10.3 mm. ท่อแกนรอง 2; CHS 300x10.3 mm.

คำนวณหาค่าฟังก์ชั่น

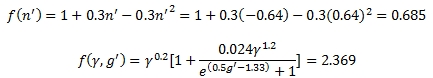
1.การตรวจสอบ Chord plastification

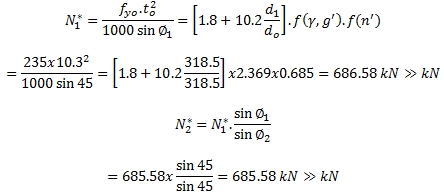
2.การตรวจสอบ Punching shear

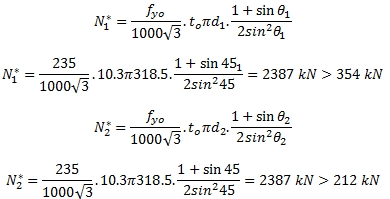
ครับเป็นเรื่องราวที่น่าสนใจไม่น้อยเลยใช่ไหมครับที่จริงนี่ยังเป็นส่วนน้อยครับเพราะยังมีการออกแบบจุดต่อของท่อในลักษณะต่างๆด้วยครับแต่ทางทีมงานยกตัวอย่างมาให้ท่านผู้เข้าชมเว็บไซต์เพียงการออกแบบจุดต่อโครงสร้างเหล็กประเภทท่อสี่เหลี่ยมผืนผ้าและท่อกลมในบางชนิด เท่านั้น ถ้าหากท่านผู้เข้าชมเว็บไซต์สนใจสามารถ ติดต่อสอบถามหรือขอข้อมูลเอกสารได้จากทางเว็บไซต์ของ บริษัท ครับ

ขอขอบคุณข้อมูลจาก บริษัท แปซิฟิกไพพ์ จำกัด (มหาชน)

เรียบเรียงโดย toyama อีบิลด

ร่วมแสดงความคิดเห็น